Confidence Limits for Regression Function

Confidence limits can be defined for the Regression Function as follows:

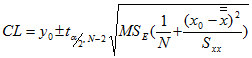
where:

N is the total number of observations

x-doublebar is the Average of the x values

Sxx is the Sum of Squares of x

MSE is the Mean Square of the Residuals

x0 is any possible value of x

y0 is the predicted value of y at x0 (based on linear regression equation)

tα/2,N-2 = value of the student t-distribution for a 100(1-α) percent of confidence interval with N-2 degree of freedom (Hines and Montgomery, 1980).

Note: The Confidence Limit at any value of yo, the predicted y, defines the location of the regression line. It does not indicate whether specific observations are well modeled by the line.

Learn more about the Regression tools in Six Sigma Demystified (2011, McGraw-Hill) by Paul Keller, in his online Regression short course (only $99), or his online Black Belt certification training course ($875).