Central Composite Design

Central Composite Design - (CCD) A CCD spans a set of quantitative factors with fewer points than a standard Fractional Factorial multilevel design, without a large loss in efficiency. It uses central points, extreme (corner) points and either face points or extended points. Central composite designs with face points require three levels; with extended axial points, five levels are required.

These three-level designs are often used for response surface analysis to map out the shapes of the quadratic surfaces. The center and axial points allow estimates of quadratic terms. (Recall that two-level designs only can be used to estimate linear surfaces.) Repeat center points provide an estimate of pure error.

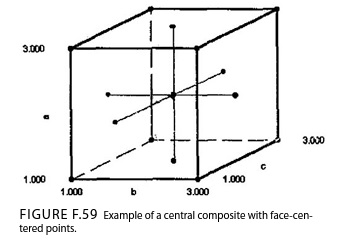
 An example of a face-centered central composite design is shown below. Note the points on the face of the cube. In this case, a standard 23 fractional factorial design is supplemented with the six face-centered points and two center points.

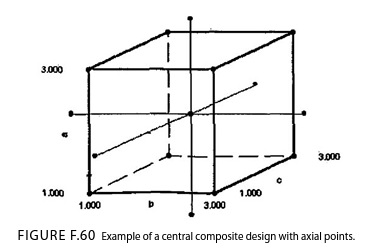
 An example of a central composite design with axial points is also shown below. In this case, a standard 23 fractional factorial design is supplemented with the six axial points and two center points.

 The location of the axial points (or more precisely, the levels of the factors) is often determined to achieve a rotatable design. Central composite designs are rotatable if the variance of the predicted response is constant at all points equidistant from the center of the design. Most central composite design software will define the axial points to achieve rotatable designs. For example, with k = 2 factors, design points are equally spaced at plus and minus 1.414, as shown in the table below.

.

.

 For central composite designs, it is not uncommon for the data to be collected in blocks owing to the size of the experiment. For example, we may begin with a screening fractional factorial and then add center and axial points.

 Recall that orthogonal designs are designs that allow all parameters to be estimated independently. Orthogonal blocking implies that the block effects do not affect the ability to estimate parameters independently. In blocked central composite designs, the choice of the axial point locations and the number of center point replicates affect orthogonal blocking.

 The recommendations suggested for central composite designs with blocking are shown in Table T.26. The last column refers to a half-fractional design for five factors.

Table T.26

Learn more about the DOE tools for designed experiments in Six Sigma Demystified (2011, McGraw-Hill) by Paul Keller, in his online Intro. to DOE short course (only $99) or online Advanced Topics in DOE short course (only $139), or his online Black Belt certification training course ($875).