Hypothesis Test Of Sample Mean Example

The following is an excerpt from The Quality Engineering Handbook by Thomas Pyzdek, © QA Publishing, LLC.

Experiment: The nominal specification for filling a bottle with a test chemical is 30 cc. The plan is to draw a sample of n=25 units from a stable process and, using the sample mean and standard deviation, construct a two-sided confidence interval (an interval that extends on either side of the sample average) that has a 95% probability of including the true population mean. If the inter-val includes 30, conclude that the lot mean is 30, otherwise conclude that the lot mean is not 30.

Result: A sample of 25 bottles was measured and the following statistics computed

The appropriate test statistic is t, given by the formula

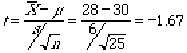
Table 6 in the Appendix gives values for the t statistic at various degrees of freedom. There are n-1 degrees of freedom. For our example we need the t.975 column and the row for 24 df. This gives a t value of 2.064. Since the absolute value of this t value is greater than our test statistic, we fail to reject the hypothesis that the lot mean is 30 cc. Using statistical notation this is shown as:

H0: m = 30 cc (the null hypothesis)

H1: m is not equal to 30 cc (the alternate hypothesis)

α = .05 (type I error or level of significance)

Critical region: -2.064 ² t0 ² +2.064

Test statistic: t = -1.67.

Since t lies inside the critical region, fail to reject H0, and accept the hypothesis that the lot mean is 30cc for the data at hand.

Learn more about the Statistical Inference tools for understanding statistics in Six Sigma Demystified (2011, McGraw-Hill) by Paul Keller, in his online Intro. to Statistics short course (only $89) or his online Black Belt certification training course ($875).