Tools
Intervals & Tests
Hypothesis Test Of Sample Mean Example
Hypothesis Test Of Two Sample Variances Example
Hypothesis Test Of A Standard Deviation Compared To A Standard Value Example
Distributions
Area Under the Standard Normal Curve
Non-Normal Distributions in the Real World
Rayleigh Distribution for True Position
Johnson Distributions
The Johnson system of distributions, published by statistician N.L. Johnson in 1949, is perhaps the most versatile choice. Johnson distributions are based on a transformation of the standard normal variable, and includes four forms:
1. Unbounded: the set of Johnson distributions that go to infinity in both the upper or lower tail.
2. Bounded: the set of Johnson distributions that have a fixed boundary on either the upper or lower tail, or both.
3. Log Normal: a border between the Unbounded and Bounded distribution forms.
4. Normal: a special case of the Unbounded form.
The flexibility provided by the choice of form and fitting parameters allows for great flexibility in adjusting the curve to fit the data. The fact that the Johnson system involves a transformation of the raw variable to a Normal variable allows estimates of the percentiles of the fitted distribution to be calculated from the Normal distribution percentiles, for use in control limit calculations (on the Individual-X chart) or for Capability Analysis. Thus, although capability indices and control limits are generally only defined for normal variables, this approach allows their calculation for all distribution types.
One of two methods is used to fit the curve to the data: the Four-Point Method or the All-Point Method. The Four-Point method does well for large data sets, since it tends to smooth the data in fitting the distribution. The All-Point method takes more time because the fit must be made at all data values rather than just the four percentile points.
It should be noted that regardless of the method used, all the data values are used, they are just used differently. The four percentile method has been shown to be nearly identical to the all points method for these larger files. However, the All-Points method is generally recommended for overall accuracy considerations, and given the speed of computers, the trade-off in speed is not that great of an issue.
The Cumulative Distribution Function of the transformed standardized normal variable z is (Hahn & Shapiro; Johnson (1983)):
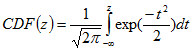
where
- ∞ < z < + ∞ and z is distributed N(0,1)
Normal form (Sn): ![]()
Log Normal form (Sl): ![]()
![]()
Unbounded form (Su): ![]()
Unbounded form (Sb): ![]()
and for computational reasons, the data values, x are first transformed to standardized values:
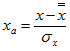
For more information on the Johnson system, refer to Johnson (1949, 1983) and Pyzdek (1991a, 1992b).
Learn more about the Statistical Inference tools for understanding statistics in Six Sigma Demystified (2011, McGraw-Hill) by Paul Keller, in his online Intro. to Statistics short course (only $89) or his online Black Belt certification training course ($875).





