Population versus Process Statistics

An excerpt from Statistical Process Control DeMYSTiFied (McGraw-Hill, 2011) by Quality America president Paul Keller. Used by permission.

Consider for example the conversion rate for a sales process. A point estimate of the conversion rate is obtained by dividing the number of actual sales by the number of potential sales in a given time period. For example, if 300 sales prospects in September resulted in 98 sales, then the conversion rate is calculated as 98 divided by 300 or 32.7%.

While the point estimate itself is useful, it lacks context: Is this 32.7% better than expected, or worse? Comparisons using statistical inference can be constructed to evaluate the sample data relative to prior experience.

A confidence interval for the proportion can be calculated as the range 27.4% to 38.3% (assuming normality), using confidence interval for proportion techniques, such as described in Keller (2011). Since this interval includes the historical estimate of 33.0%, there is no evidence the sample differs significantly from the past experience.

Similarly, a hypothesis test for two proportions, such as found in Minitab, can be used to determine if September’s conversion rate is equivalent to the historical conversion rate. In this case, the historical data consisted of approximately 9000 prospective clients over 30 months, of which nearly 3000 were converted into sales. The hypothesis test yielded a p-value of 0.91, suggesting that samples this extreme would occur 91% of the time if the conversion rates were equal. In other words, there is no evidence that the conversion rates are different. (Note: We would typically look for a p-value of 0.05 or less to suggest the conversion rates were different).

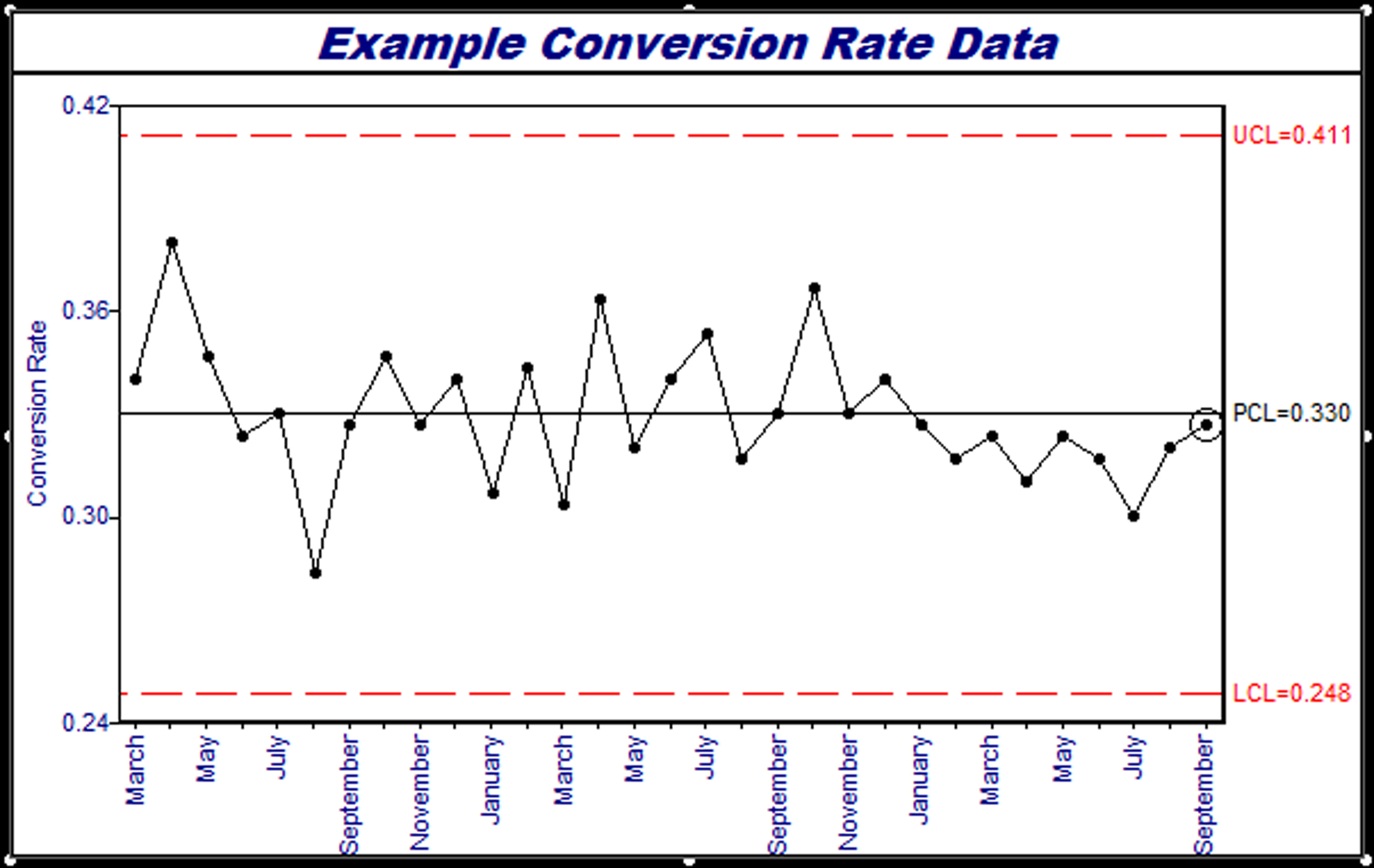
Figure 1.1 - Example control chart of sales conversion process.

A control chart of these 31 months of data is shown in Figure 1.1. This particular control chart is referred to as a p chart, where p refers to percent. It is the preferred chart when plotting percentages, and will be discussed in more detail later in the book.

All control charts have the following properties, which are evident in Figure 1.1:

1. The x-axis is a time-ordered sequence, with earlier data on the left and the most recent data at the far right of the chart. Note in Figure 1.1 the x-axis is scaled by months, where each plotted point represents the summarized data for a sample taken that month.
2. The y-axis is scaled to the statistic charted for each point in time. Figure 1.1 charts the conversion rate.
3. Statistical control limits are defined for the plotted statistic based on process data. The limits are never determined using customer specifications or management goals. In Figure 1.1 the upper control limit (labeled UCL) is calculated as 0.411; the lower control limit (labeled LCL) is calculated as 0.248. (The calculation methods for these statistics are dependent on the type of chart, as discussed later in the book for each chart type.)
4. The statistical control limits are determined by estimating the “short-term” variation in the process. Statistical process control is synonymous with stability and is achieved when the short-term variation provides a good model (or estimate, or prediction) of the longer-term variation.
5. The calculated statistical control limits provide an indication of the expected bounds of the plotted statistic. This expected variation (between the control limits) is intrinsic (built in) to the process. This inherent process variation is usually referred to as common cause variation, since the sources of variation are common to all plotted points within the control limits. Although the actual sources of variation (and their relative contribution) may be unknown, their effect on the process is systematic and consistent over time, allowing prediction of the future performance of the process. If the control limits defined in Figure 1.1 are representative of the conversion rate process, the conversion rate is expected to vary between 24.8% and 41.1%.
6. When plotted points exceed the control limits, they are influenced by special causes of variation. This is evidence that the process has shifted or changed, at least for the time period evidenced by the points beyond the control limits. When special causes exist, the process is out of control. A key value of the control chart is to identify the occurrence of special causes so that the process knowledge can be gained concerning the sources of special causes and corresponding corrective and preventative action taken for process improvement.
7. In the absence of special causes, the process is in control. The control limits are calculated such that the chance of plotted points exceeding the upper or lower control limit is very small unless the process has changed.
8. In addition to the control limits, statistical run test rules can also be applied as appropriate to test for unlikely conditions indicative of a special cause. These run test rules enhance the sensitivity of the control chart by looking for unnatural data patterns within the control limits. In Figure 1.1, note how the last plotted point (September’s data) is circled, which this software uses to indicate a violation of one of the run test rules. In this case, the chart detected that nine points in a row were beneath the center line of the process. The chance of this happening if the process had not been subject to a special cause of variation is extremely rare (less than 2/10 of 1%). The implication is that the process has changed, perhaps as early as January (the first of the nine plotted groups in a row beneath the center line). When a sustained process shift is identified and confirmed in process terms, the control limits can be adjusted as shown in Figure 1.2 to reflect the new process conditions.



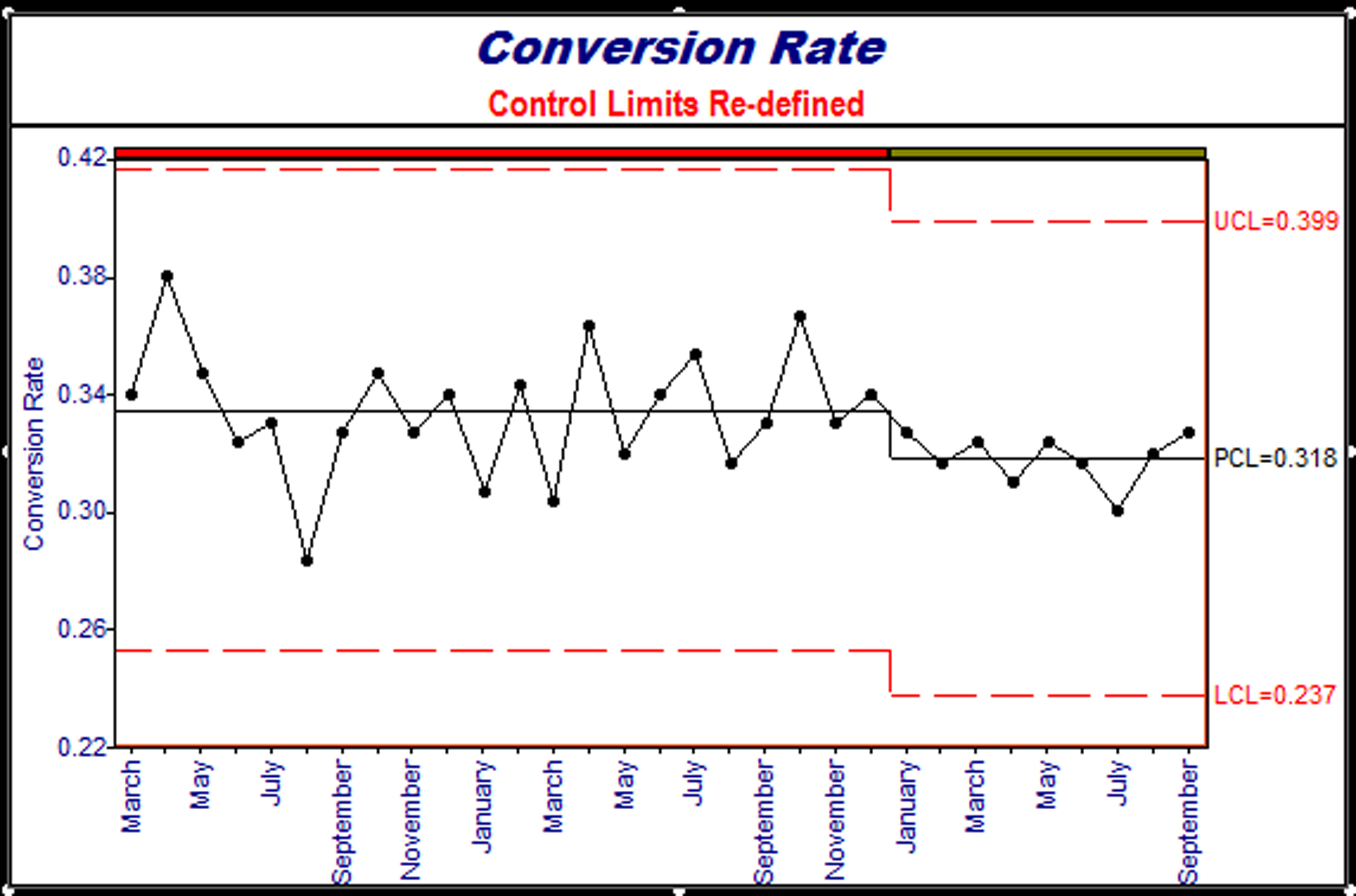
Figure 1.2 - Example sales conversion process with sustained process shift.

It should be clear that the control chart identified a process shift that was undetected by the classical statistical methods. These classical methods, including statistical inference tools of confidence intervals and hypothesis testing as well as histograms, ignore the sequencing of the process data which in many cases provide valuable additional information. The classical statistical tools are developed for fixed populations and not for processes.

The confidence intervals and hypothesis tests cited earlier in the example pooled the data and ignored their sequence. Process control charts add the element of time to the analysis: This additional dimension takes advantage of the inherent time sequencing of data produced by a process.



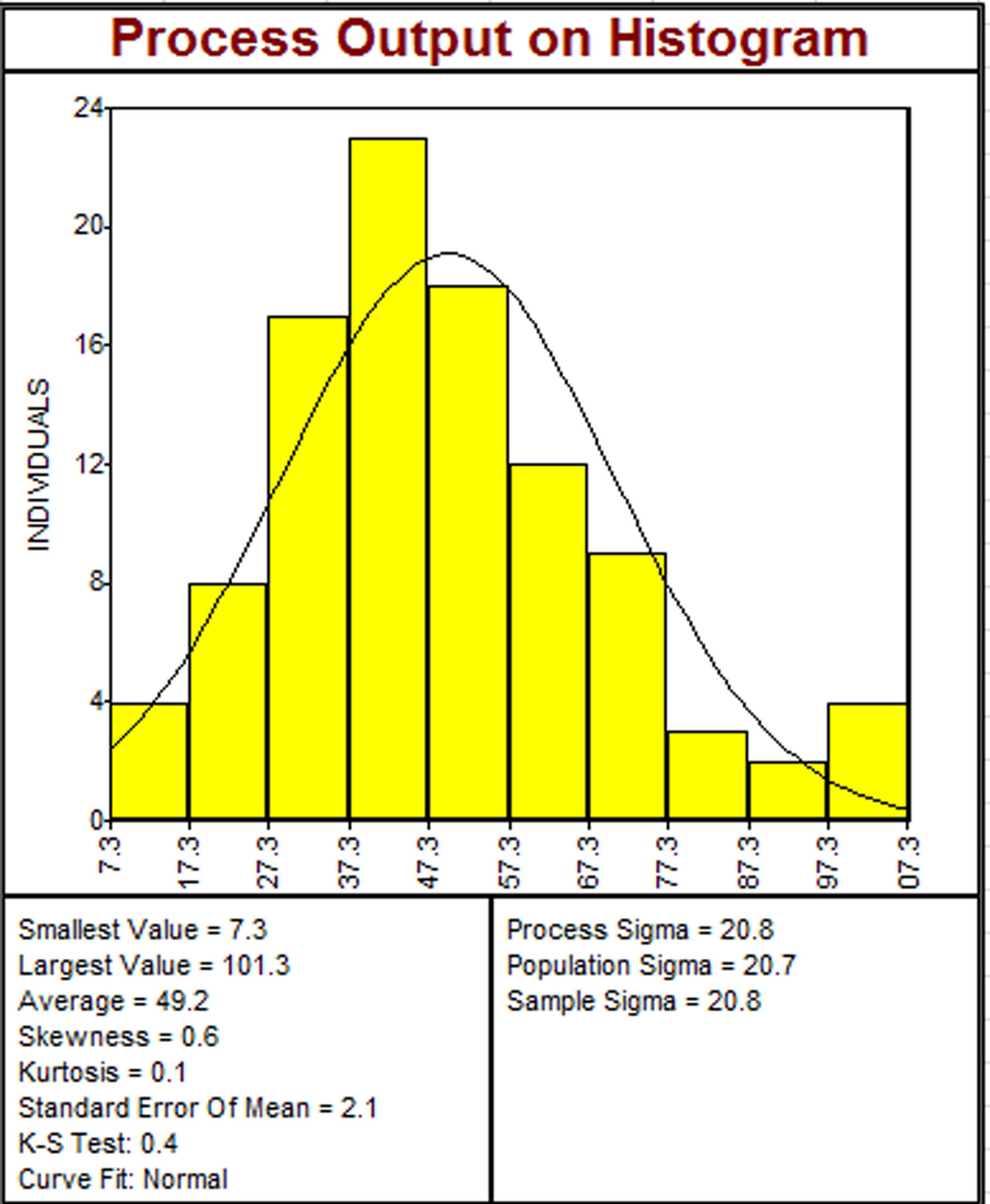
Figure 1.3 - Histogram with the intent to show a stable and capable process.

Similarly, process histograms have become the graphical equivalent of the damned lies and statistics. [Editor's Note: See note at bottom]. The histogram is an enumerative tool: Even when process data is properly collected for analytical use, its time sequence is lost as the data is collapsed into the histogram cells. Consider the histogram shown in Figure 1.3. Note the well-defined bell-shaped curve, and its positioning well within the customer’s upper specification limit (USL) and lower specification limit (LSL). Obviously this process is well-controlled, stable, and capable of meeting the customer requirements.



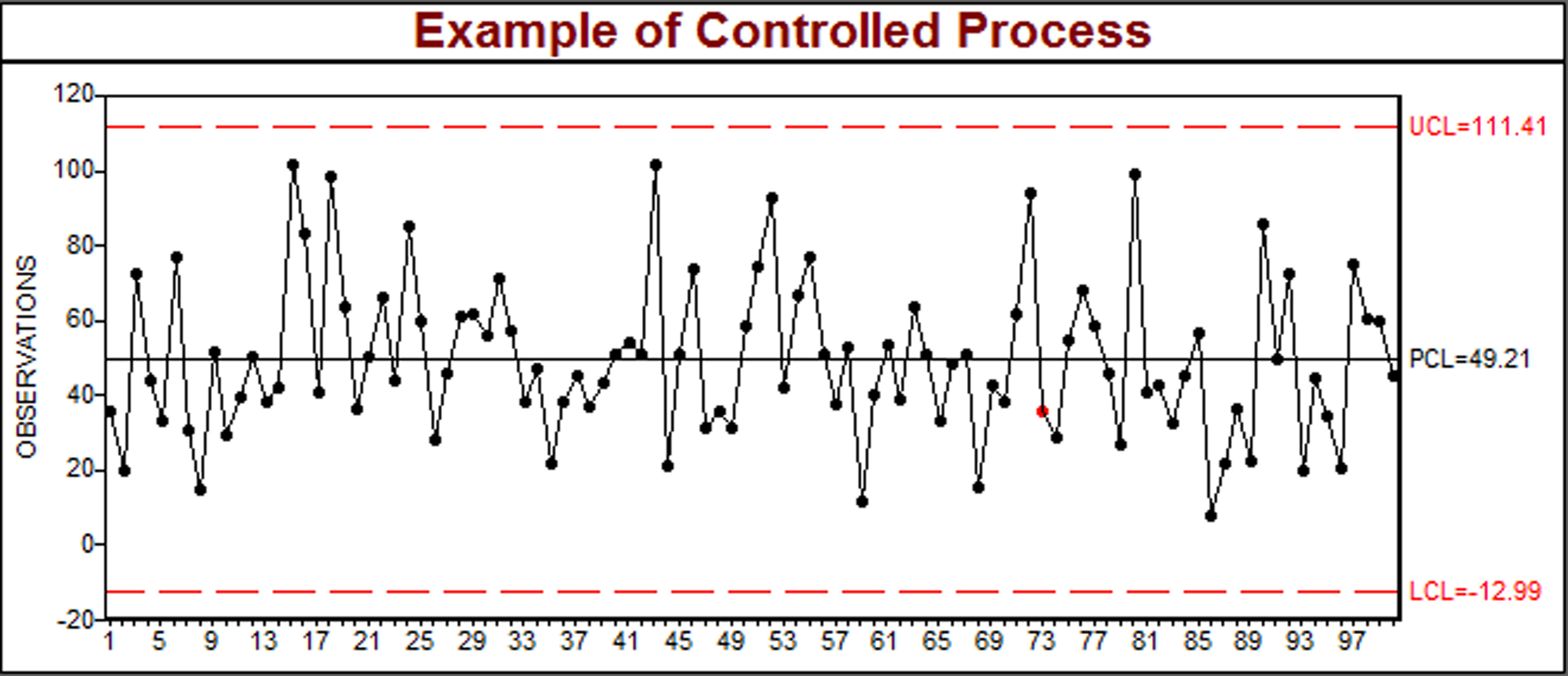
Figure 1.4 - One of many possible processes producing the histogram of Figure 1.3.

Or perhaps not. The processes shown in Figures 1.4 and 1.5 contain the identical data used to construct the histogram. Clearly, even with limited understanding of control charting, it is apparent that the processes associated with Figures 1.4 and 1.5 are quite different. Figure 1.4 shows a stable process operating within its statistical control limits; Figure 1.5 shows a process trending in a positive direction. Will its next sample be even larger? Or perhaps the cycle will start over again? Or something else? There is no way to know, since the process is out of control! By definition, it is unpredictable.



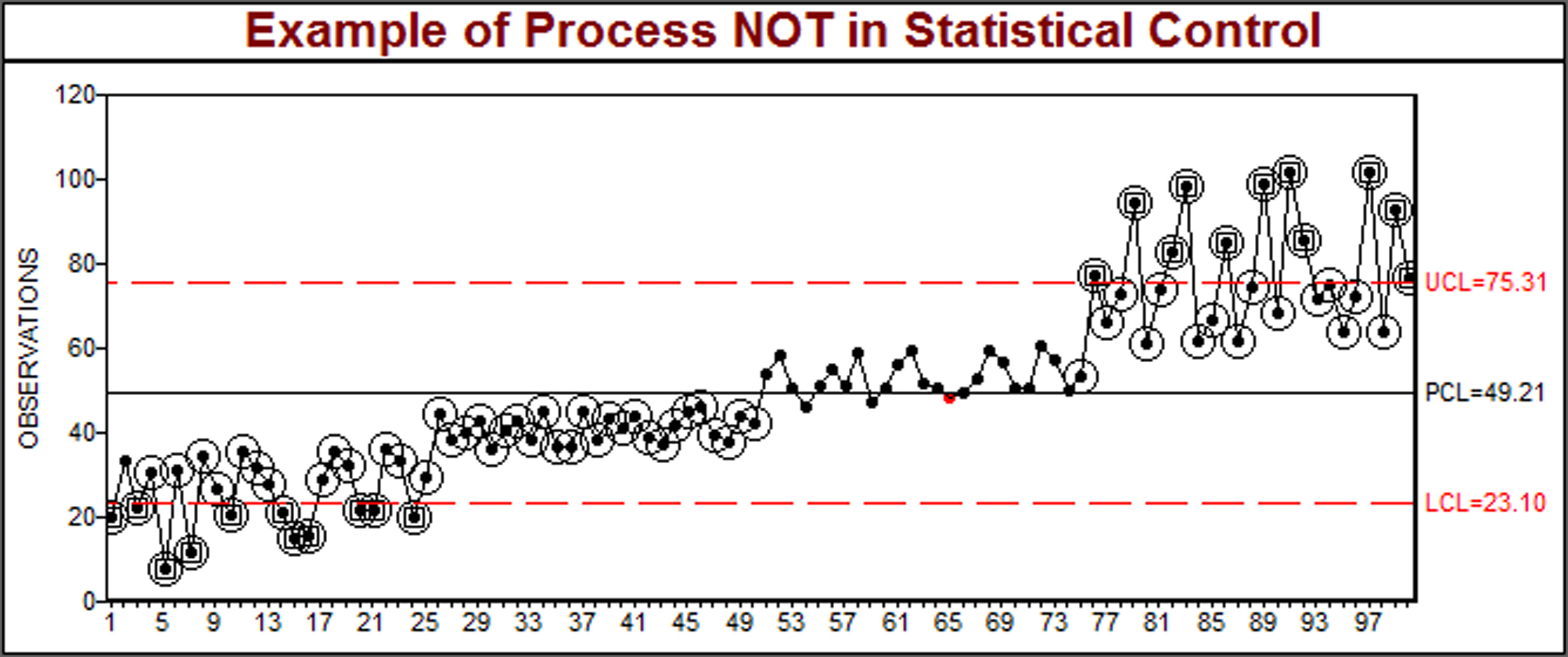
Figure 1.5 - A less favorable process producing the histogram of Figure 1.3.

Histograms can never be used to show process stability, or even conformance to requirements. The control chart is the only tool that can serve those purposes. Unlike the histogram, confidence intervals and hypothesis tests, only the control chart is capable of predicting future process behavior. Generally, a histogram should not be used without a control chart, unless the data used to construct the histogram is census data (i.e., 100% of all possible units in the study). When there is no time sequence to the data, such as when data is sampled from a supplier’s shipment, a histogram can be used to graphically show the distribution of the sample, whose interpretation is subject to the limitations of sampling statistics. Those limitations include 100% sampling (i.e., all output is measured and verified) if the process has not been shown to be in statistical control.

Editor's Note: The reference is to an earlier discussion of a quote attributed to Samuel Clemens (aka Mark Twain), who popularized the notion of the misuse of statistics as the worst of three possible types of mistruths: “lies, damned lies, and statistics.” It should be clear that Twain was referring to the misuse of statistics, and not the general use of statistics to define an issue or assist in problem-solving.

See also:

Enumerative and Analytic Studies




Learn more about the SPC principles and tools for process improvement in Statistical Process Control Demystified (2011, McGraw-Hill) by Paul Keller, in his online SPC Concepts short course (only $39), or his online SPC certification course ($350) or online Green Belt certification course ($499).