Process Performance Indices

The following is an excerpt from The Quality Engineering Handbook by Thomas Pyzdek, © QA Publishing, LLC.

Some have advocated computing the process capability indices even when the process is not in a state of statistical control. Although the formulas used are the same, the standard deviation used is not based on the control chart. Instead the formula for the standard deviation used is the one shown in the equation below.

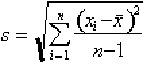
When this analysis is performed on processes that are not in statistical control the indices are called process performance indices (PPIs). They cannot properly be called process capability indices (PCIs) since when s is computed from the equation above, it includes variability from special causes of variation as well as variation from common causes. When the special causes are identified and eliminated the process will do better, which implies that the process capability is better than the process performance index indicates.

A PPI is intended to show how the process actually performed, rather than how well it can perform under properly controlled conditions. Thus, in a sense, PPIs are designed to describe the past while PCIs are designed to predict the future. The difference between a PPI and its corresponding PCI is a measure of the potential improvement possible from eliminating special causes.

I have serious reservations about using PPIs. First of all, if the process is not in a state of statistical control the future cannot be predicted from the past, that is what statistical control means! An out-of-control process has no underlying distribution, it is a mixture of distributions in unknown proportions. And since the special causes are unknown, there is no basis for predicting which distribution will appear next or how long it will last. PPIs assume the process distribution is normal, even though we do not even have a process distribution!

That being the case, what is the point of a PPI? So what if a PPI indicated that for a particular run the process met the requirements, or did not meet the requirements? Since the future cannot be predicted, the only possible reason for caring is the quality of the current production lot. Using a PPI to estimate lot quality is futile because of the vagaries of estimating parameters with statistics, fitting curves, finding the relationship between the specification zone and the statistical distribution, etc. Even the much maligned acceptance sampling approach provides a much better way to estimate the quality of a production lot from an out of control process than a PPI. And a simple, but expensive, sorting operation will tell you exactly what it did.

Ascribing meaning to an index, either a PPI or a PCI, always depends implicitly on knowing the underlying distribution. This knowledge can be based on engineering knowledge (preferably) or on empirical evidence. However, if the process is not in control then, by definition, there is no "distribution" per se. There are two or more distributions mixed together. The causes of the distributions are not generally known for out-of-control processes. Given the difficulties associated with capability analysis of homogeneous output, analysis with unknown proportions of output from unknown distributions is virtually impossible.

If PCIs suffer because they only measure process capability indirectly, how much worse are PPIs which are not even indirectly related to yields? This is because they are computed from data that represent a mixture of several unknown process distributions. To compute the yield, you would need to know the characteristics of each separate process and their representation in the sample. If you knew that, you could probably identify what the special causes were and you could remove them, achieve a state of statistical control, and compute a PCI instead of a PPI.

It is best to spend your time finding and correcting the special causes; then PPIs are not needed.

Learn more about the SPC principles and tools for process improvement in Statistical Process Control Demystified (2011, McGraw-Hill) by Paul Keller, in his online SPC Concepts short course (only $39), or his online SPC certification course ($350) or online Green Belt certification course ($499).