Rational subgroup sampling

The following is an excerpt from The Six Sigma Handbook: Fourth Edition (McGraw-Hill 2014) by Paul Keller and Thomas Pyzdek.

The basis of all control charts is the rational subgroup. Rational subgroups are composed of items which were produced under essentially the same conditions. The statistics, for example, the average and range, are computed for each subgroup separately, then plotted on the control chart. When possible, rational subgroups are formed by using consecutive units. Each subgroup's statistics are compared to the control limits, and patterns of variation between subgroups are analyzed. Note the sharp contrast between this approach and the random sampling approach used for enumerative statistical methods.

To understand the concept of rational subgrouping, it's useful to understand the role of the subgroup in the control chart. The subgroup provides a snap shot of the process at that moment in time. On an averages (aka X-bar) chart, for example, each subgroup provides an estimate of the process location, while the range (or sigma) chart provides the subgroup estimate of the short-term variation. The control limits on the averages chart are defined based on the average within-subgroup variation (estimated using the average within-subgroup range, for example), and when the short-term within- subgroup variation predicts the longer-term between-subgroup variation, then the process is in statistical control. When the longer-term variation is not predicted by the short-term within- subgroup variation, then a special cause has been identified, or more precisely, operationally defined.

A fundamental aspect of the subgroup is thus to estimate the common cause variation within the process, since the within-subgroup variation is used to define the width of the control limits. Therefore, it is critical that the causes of within- subgroup variation be representative of the causes of variation between subgroups. This is not to say that each and every subgroup must contain an identical subset of causes of process variation. Rather, the system that defines the causes is consistent. Consider the following cases:

Measure the fill volume of each of the six bottles of beer filled by a multiple-head filling station, grouping the six measurements into a subgroup. Take data for a new subgroup (i.e., a different set of bottles from the same six heads) every hour.
Measure the thickness of an extruded plate. Since the plate thickness can vary across its width, measure at three locations to form the subgroup. Take data for a new subgroup (i.e., at a different location along the length) every 10 minutes.

In each of these examples, the subgroup is not rational, since a different system of causes influences the within-subgroup variation than influences the between-subgroup variation. In the beer filling operation, the variation in fill volume is influenced by head-to-head differences. A consistent difference in nozzle size or line pressure in one head versus the others will cause the within-subgroup variation to be excessively large, masking any longer-term variation in fill volume for any of the individual heads. This produces the characteristic behavior noted in Fig. 8.23: Many subgroups hugging the centerline of the averages chart. (The circled values are violations of Run Test 7, discussed in the next section, which is used to detect this error in subgrouping).

Fig 8-23: Centerline
hugging evidence of irrational subgrouping in X-bar /Range chart

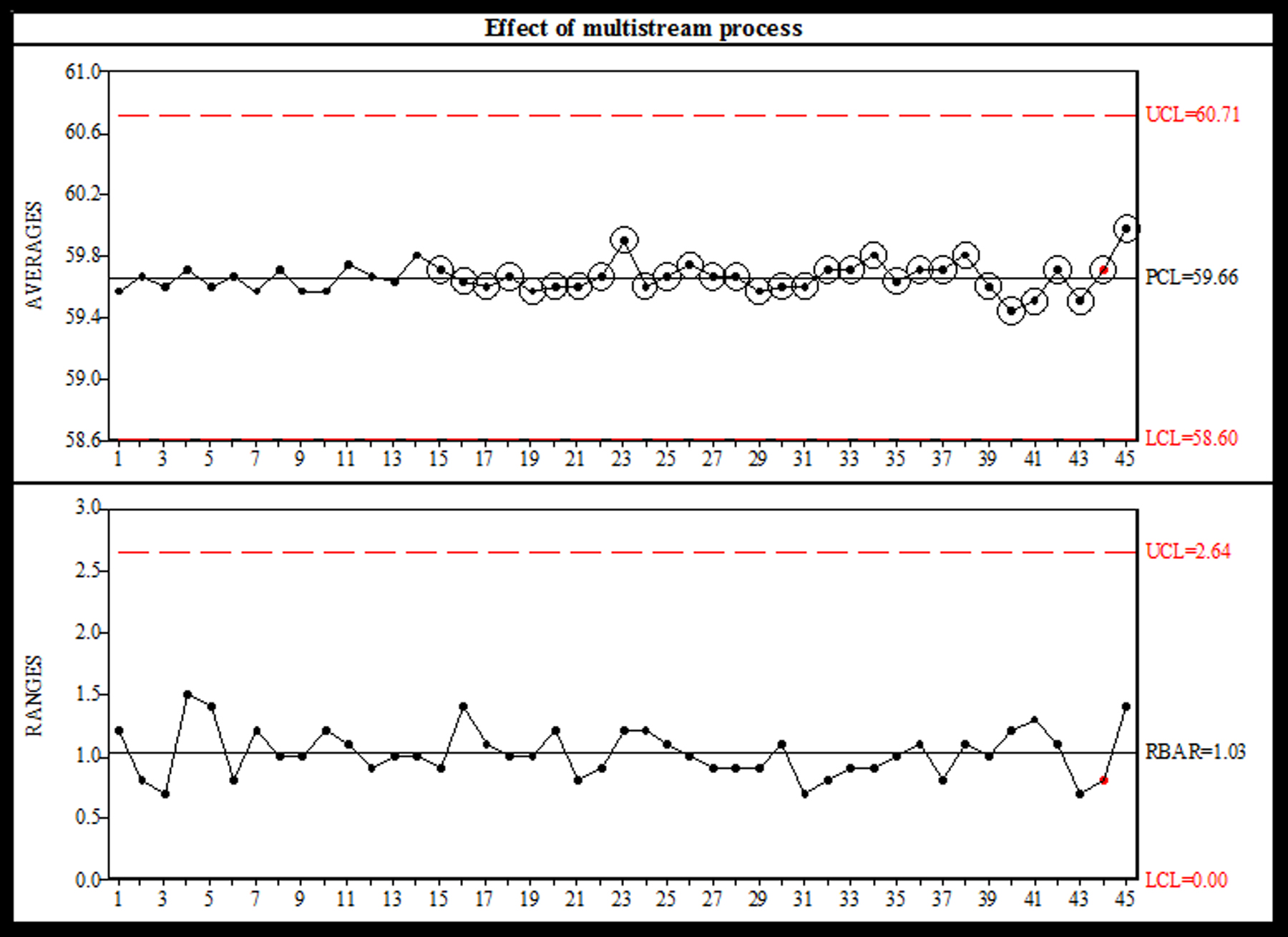
SPC-PC IV Software detects irrational subgroups in X-bar /Range chart

A solution to the centerline hugging is offered with a special version of a chart sometimes referred to as a Batch Mean chart. (Minitab refers to this chart as the Between-Within Chart.). The range (or sigma) chart is used to monitor the process variation, as usual, but the averages chart is replaced with an Individual-X chart, whose control limits are based on the moving range between the subgroup averages. The data from Fig. 8.23 is plotted with the Batch Means option as shown in Fig. 8.24.

Fig 8-24: Batch
Means analysis of Fig 8-24 data

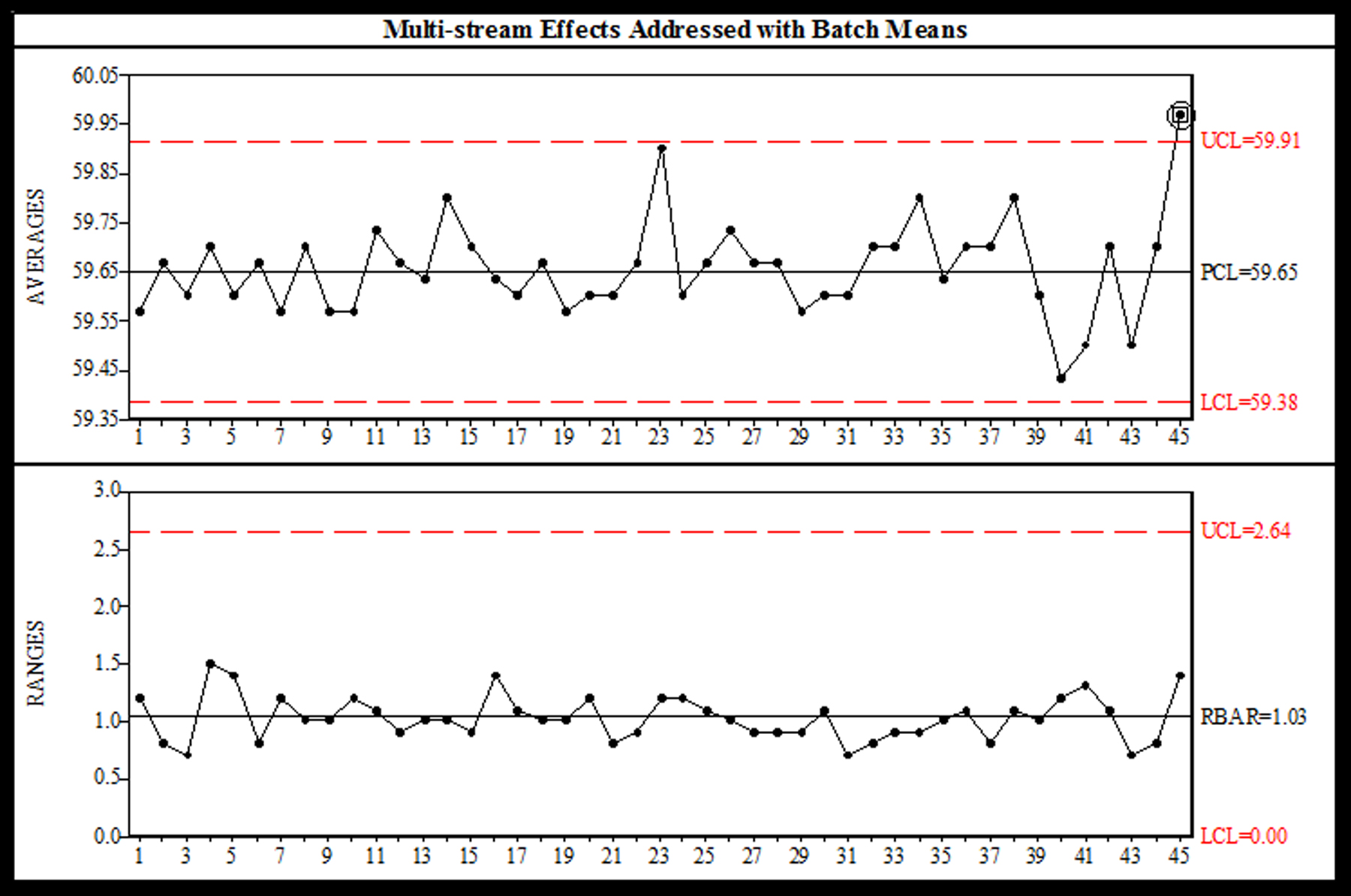
SPC-PC IV Software displays Batch Means chart with irrational subgroups

The idea of rational subgrouping becomes a bit fuzzy when dealing with X charts, or individuals control charts. The reader may well wonder about the meaning of the term subgrouping when the subgroupÂ is a single measurement. The basic idea underlying control charts of all types is to identify the capability of the process. The mechanism by which this is accomplished is careful formation of rational subgroups as defined above. When possible, rational subgroups are formed by using consecutive units. The measure of process variability, either the subgroup standard deviation or the subgroup range, is the basis of the control limits for averages. Conceptually, this is akin to basing the control limits on short-term variation. These control limits are used to monitor variation over time.