Moving Range Chart Calculations

Plotted statistic

The moving ranges between successive subgroups in an Individual-X Chart (i.e.: the difference between the current observation and the observation immediately prior).

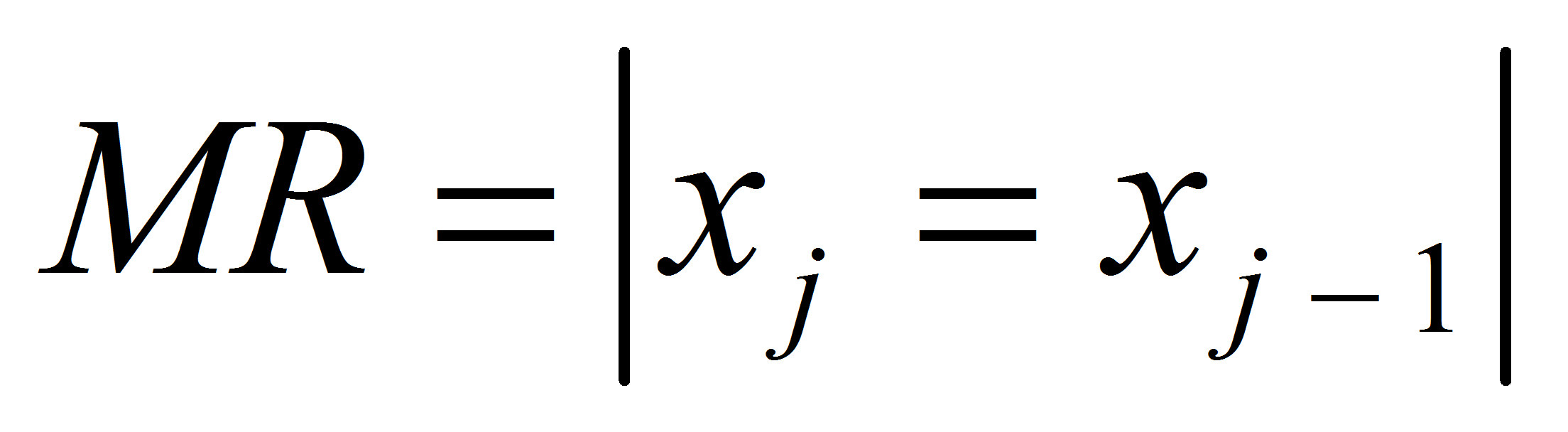
Center Line

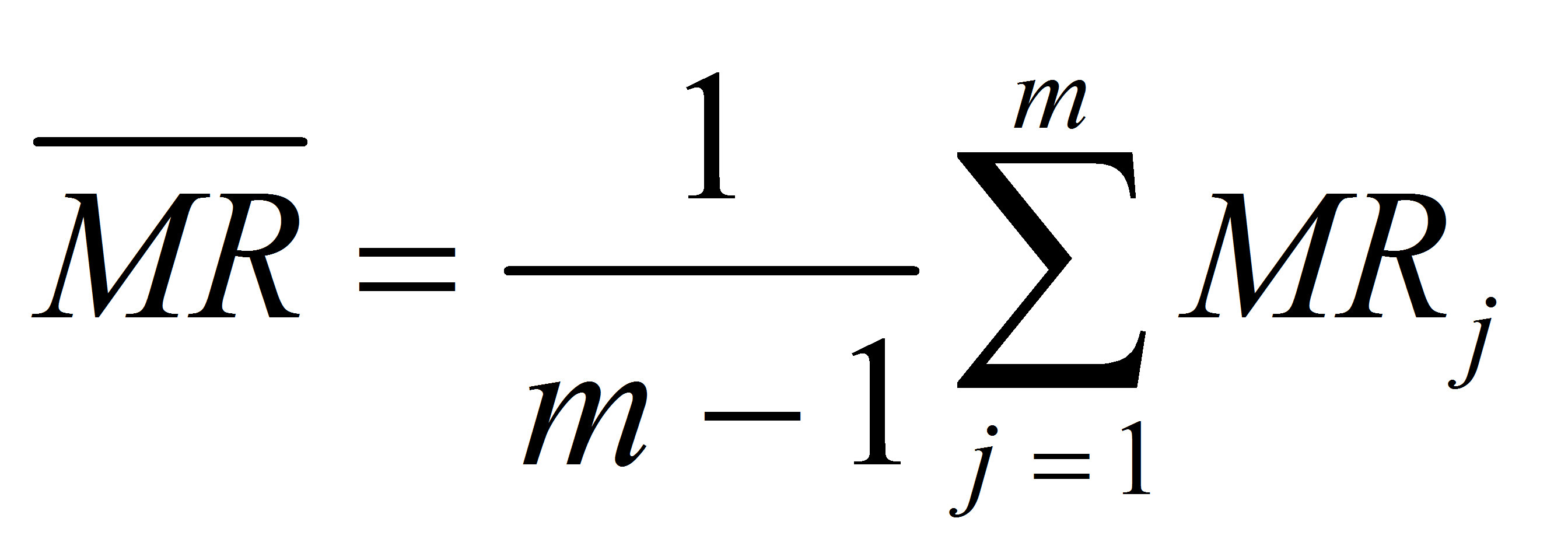
where m is the total number of subgroups included in the analysis and MRj is the Moving Range at subgroup j.

Note: When control limits for the Individual-X chart are defined as fixed values (such as when historical data is used to define control limits), the Average Moving Range (MR-bar) must be back calculated from these pre-defined control limits. This ensures that the control limits on the Moving Range chart are at the same sensitivity as those on the Individual-X chart. In this case:

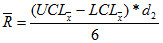
where d2 is based on n=2.

UCL , LCL (Upper and Lower Control Limit)

UCLMR = 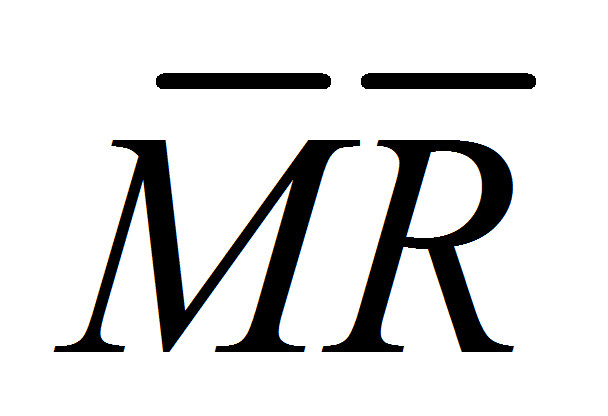+ 3d3σx (All Distributions)

LCLMR =MAX(0, 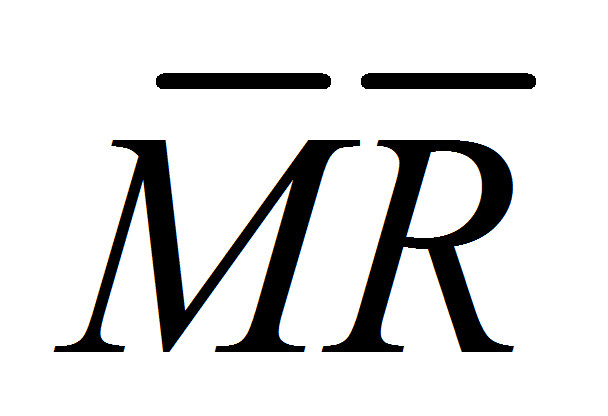- 3d3σx) (All Distributions)

where MR-bar is the average of the plotted Moving Range values, sigma-x is the process sigma , and d3 equals 0.853.

Notes: Some authors prefer to write this as:

UCLMR =3.267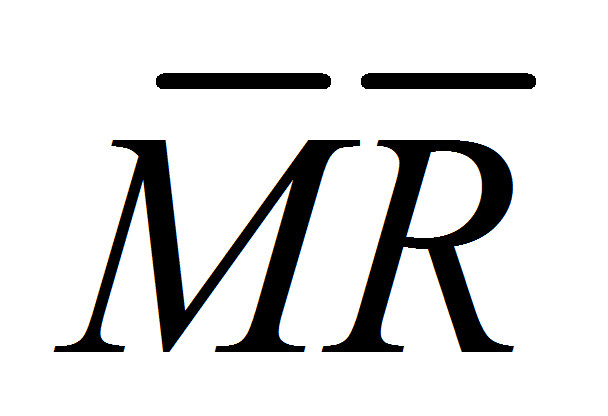

LCLMR =0

Learn more about the SPC principles and tools for process improvement in Statistical Process Control Demystified (2011, McGraw-Hill) by Paul Keller, in his online SPC Concepts short course (only $39), or his online SPC certification course ($350) or online Green Belt certification course ($499).